Normalized Cross-Correlation
By TC
Description
Normalized Cross-Correlation (NCC) is by definition the inverse Fourier transform of the convolution of the Fourier transform of two (in this case) images, normalized using the local sums and sigmas (see below). There are several ways of understanding this further, a very simple example is that this normalized cross-correlation is not unlike a dot product where the result is the equivalent to the cosine of the angle between the two normalized pixel intensity vectors. In addition to this, the normalized cross-correlation used here is essentially a Pearson product moment correlation, where the expected value of the convolution of the data sets is defined as the inverse Fourier transform of the convolution of the two Fourier transforms (The equation below for nXcorr should now look more familiar). This type of correlation is a very standard statistical analysis tool to ascertain the agreement between two data sets, and Fourier transforms are used here purely for convenience and speed. The direct dot product or pure convolution could likewise be used, but these are much slower.
Thankfully you don't need to understand any of that to make it work. A brief description of the algorithm is provided below, but if you don't care and just want to know how to use the program skip to the Usage section.
It is important to note that the NCC algorithm used follows directly with the MATLAB routine normxcorr2.m and for further documentation to better understand the methodology behind NCC please see Fast Normalized Cross-Correlation, Lewis 1995 and Fast Template Matching, Lewis 1995.
For instructions on running batch NCC and relevant statistics, see batchCorrelation
Algorithm
T = "template" image (This is the image you are searching for in matrix form) A = "search" image (This is the region in which you are trying to find "template") Ft = FFT(T) Fa = FFT(A) (Here FFT() denotes the fast Fourier transform. This code uses the built in FFT module in the Python Scipy library.) Xcorr = IFFT(Ft*Fa) (Here IFFT() denotes the inverse fast Fourier transform.) cSumA = cumulative_sum(A) cSumA2 = cumulative_sum(A^2) sigmaA = (cSumA2-(cSumA^2)/size(T))^(1/2) sigmaT = std_dev(T)*(size(T)-1)^(1/2) nXcorr = (Xcorr-cSumA*mean(T))/(sigmaT*sigmaA) (This is the matrix of normalized cross-correlation coefficients)
Usage
The heart of running an NCC analysis is based on one of the two python scripts: mpXcorr.py or imXcorr.py, which are what is used to calculate the correlation as well as provide some other useful information. While these two versions provide similar results, they have two different purposes. mpXcorr.py is for comparing PGM images created using the showmap routine, while imXcorr.py is for comparing PGM images created by Imager_MG, or flight like images.
Running:
python mpXcorr.py -h
or
python imXcorr.py -h
Will print out the usage header giving brief instructions to remind you of the syntax.
# USAGE: python mpXcorr.py [-option] outfile image1 image2 # # -o Use this followed by 'outfile' to # specify a unique output destination. # Default is corrOut.png if 'outfile' # is not specified. # # -h Use this to print usage directions # to StdOut. (Prints the header) # # -v Use this to only output current # version number and exit. By default # the version will be sent to StdOut # at the beginning of each use. # ########################################################
A typical invocation of this program is as follows:
python mpXcorr.py /path/to/image1.pgm /path/to/image2.pgm
Using the "-o outfile" option is not necessary and is only used if you wish to specify the name and path of an outputted png image of the correlation results. By default when "-o" is invoked the output will be corrOut.png (example shown in Output section).
If you do not specify any input image files, or command line options, you will be prompted for them as such:
You forgot to specify the image files to compare! Please enter the image filenames now:
Your answer should be two image files with their relevant paths, entered on the same line separated by a space.
Standard convention dictates that image1 be the template and image2 be the search image. Image1 should be smaller in pixel dimensions than image2, if it is not, you will receive an error, and be prompted as follows:
ERROR: Image must be smaller than search area. Template size: (401, 401) Would you like to sub-sample search template? (y/n)
This output tells you the pixel dimensions of the template and asks you if you would like to sub-sample the template and continue with the calculations. The reason for this is because the Fourier transform convolution becomes meaningless along the border regions for matrices of similar dimensions (a padding of zeros is used to combat this). Responding 'n' to the above will exit the program and you may try again with a new image, responding with 'y' will then prompt you with:
Enter px/ln box (min 50px x 50px) to use as x1 x2 y1 y2:
Here you may specify the pixel and line coordinates of the four corners of a sub-region of the search template to use. The size you should pick depends on the search image but a good minimum is 100 x 100 pixels, and smaller than 50 x 50 can lead to misidentification. The dimensions you enter need not be square.
Output
Now for the good stuff! Provided you did everything above correctly you will get an output to the screen similar to the following:
mpXcorr.py version: 1.5A.2 Image to search for: send/EVAL20.pgm Image to search in: send/T15-1K.pgm Output figure file: corrOut.png Found match in search area at px/ln: 506 556 Max correlation value: 0.798877683033 Template moved dx = 6 dy = -44 pixels from center of search area. .----> +y | | v +x
Every time the program is run, the version and I/O files will be printed to the screen for traceability. Next the location of the maximum correlation value corresponding to a pixel and line in the search image is printed; followed by the correlation value [-1:1] at that location, and how far that value is from the center pixel of the search image.
This last part is very important! If you either specified a sub-sampled box that is not centered at the same location as the search image, or the template is in general not centered in the same location, these dx and dy values are meaningless! Lastly coordinate axes are printed to remind the user of the positive x and positive y convention used by SPC maplets. For the sake of the dx and dy values only, (0,0) is considered to be the center pixel of the search image. For all other pixel/line values (0,0) is the standard upper left corner.
As can be seen from the above output, a file named corrOut.png was also created in the working directory, so let's take a look at that.
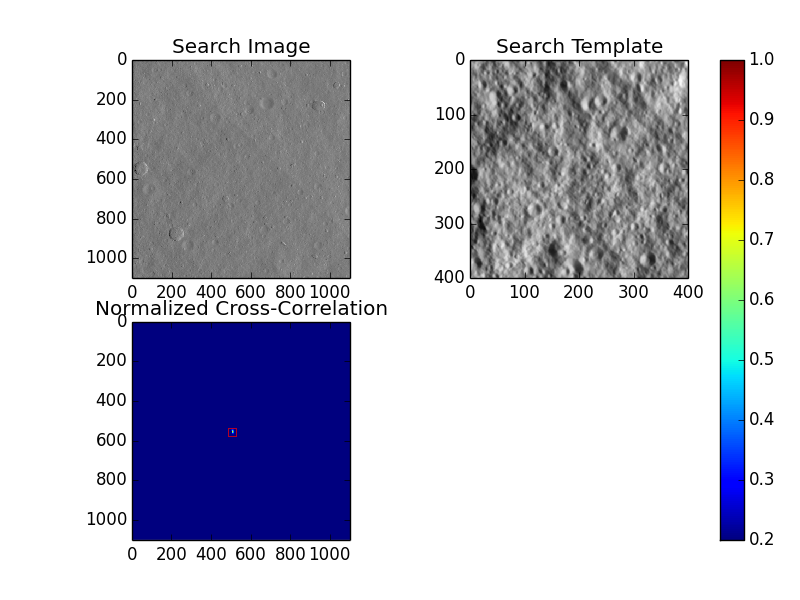
The generation of this figure requires the Python matplotlib package, but as it is not crucial to the calculation of any data, this is only generated when "-o" is invoked.
What we see in this figure is the search image in the upper left hand corner, the template to search for in the upper right hand corner, and then the correlation surface truncated from [0.2:1] in the bottom left. The colorbar is to give an approximate idea of the max correlation value, but generally the peak is very narrow and color is hard to discern. Since quite often for good data the peak is very narrow, it can be hard to spot, so a red box is also placed around it for visibility.
