Test Over11 F/G/H/I/J Comparative Results
Line Graphs
The following figures are line graphs that show measurements of CompareOBJ's calculated RMS with and without optimal rotation & translation at each iteration, CompMapVec's calculated RMS, the measured formal uncertainty at each iteration, and COmpareOBJ RMS minimum location. A discussion of the observations are discussed below each figure. Note that iteration "0" is the tiling at 5 cm step.
Figure 1: CompareOBJ's Calculated RMS
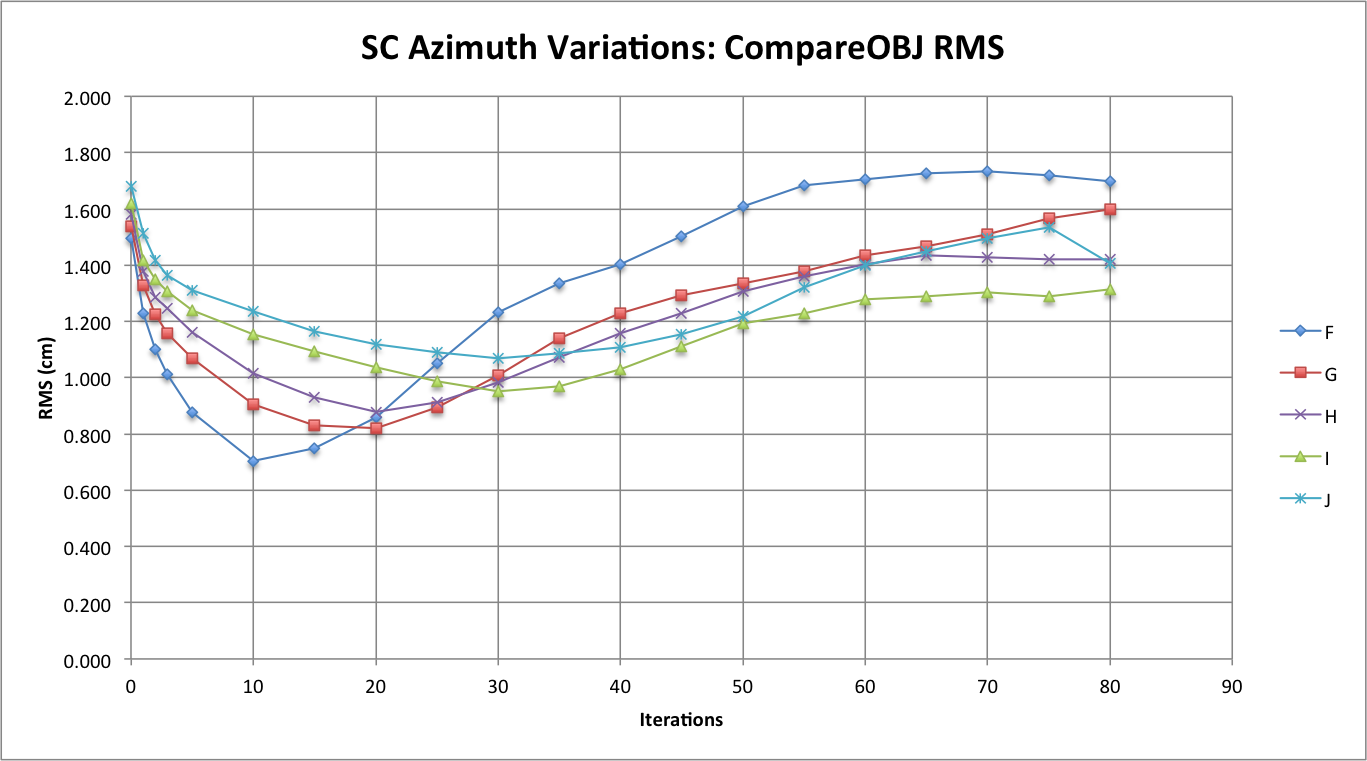
Comparing the CompareOBJ RMS between the Azimuth Variation Tests yielded very interesting results because one can clearly see the minimum CompareOBJ calculated RMS values obtained for each test. Test F has the lowest RMS minimum with it occurring the earliest and Test J has the greatest RMS with it occurring the latest. Furthermore, the other tests see to follow this trend where better azimuthal representation correlates to a lower CompareOBJ RMS minimum that occurs earlier while worse azimuthal representation correlates to a greater CompareOBJ RMS minimum that occurs later. The next to figures demonstrate this trend.
Before Discussing the next figures, one more observation that can be made from Figure 1 is that at the higher iterations Tests F, H, and I seem to converge (or at least seem steady), while Tests G and J do not converge. The RMS of Test G appears to still be increasing while the RMS of Test J hits an inflection point at iteration 75 and decreases. If Test J is disregarded, one could conclude that the better the azimuthal representation the greater the CompareOBJ RMS at higher iterations. However, since the sample is so small (because only 4 tests) the conclusion just made is not very strong. Furthermore, it is unknown whether Tests J's change in inflection at high iterations is common at azimuth representation above every 60 degrees.
Figure 2: CompareOBJ's Calculated RMS Minimum Occurrence
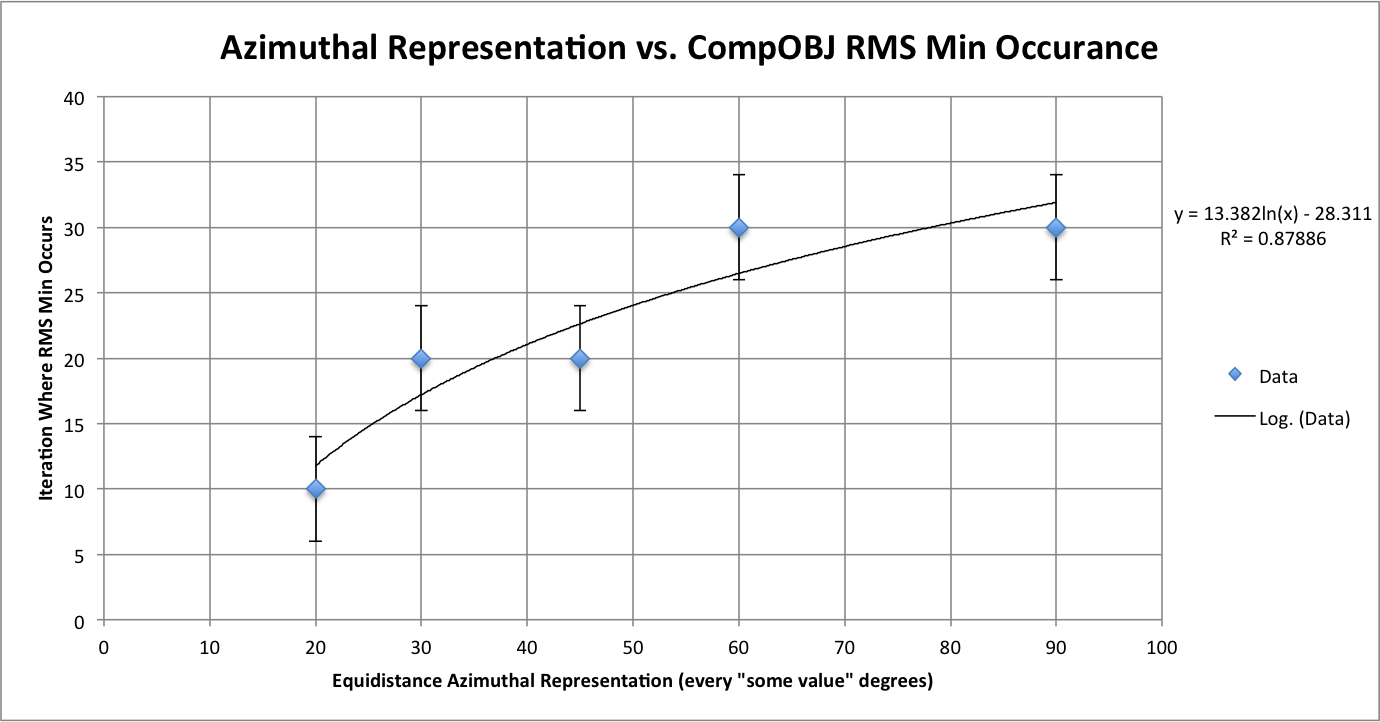
Figure 2 Shows how equidistance image azimuth representation affects where CompareOBJ's RMS minimum occurs in the iterative process. Error bars were added to the line graph to show that the iteration where the minimum occurs is at most a distance of 4 from the value measured. The error bars basically are there to let the observer know that measurements were taken every 5 iterations. Also, a trend line was added to the figure to demonstrate where the RMS minimum occurrence would be for equidistance azimuthal representations not tested. It is important to note that the trans line selected is logarithmic because a logarithmic trend line gave the best correlation with data and it fell in within the error bars of all the data points. This graph clearly demonstrated one of the observations from Figure 1 where better azimuthal representation leads to an earlier CompareOBJ minimum and vice versa.
Figure 3: CompareOBJ's Calculated RMS Minimum Value
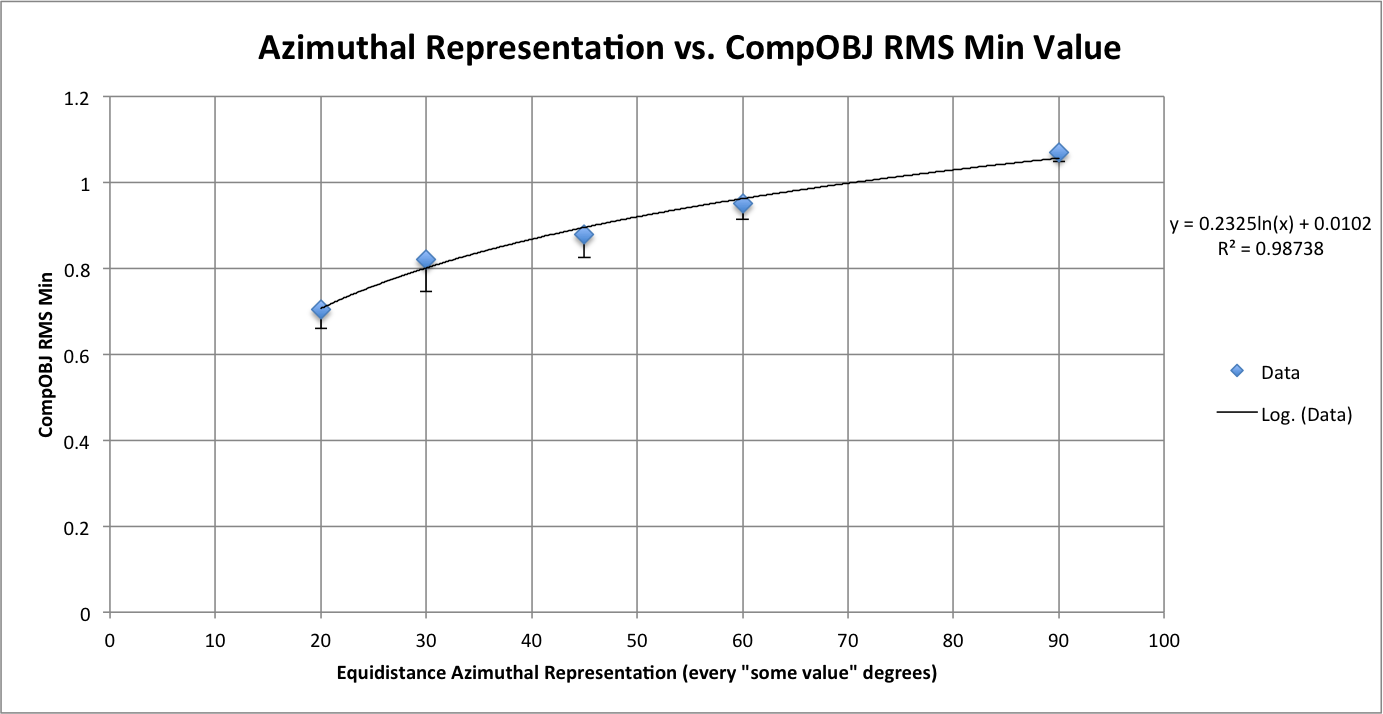
Figure 3 shows how equidistance image azimuth representation affects CompareOBJ's RMS minimum value. Like Figure 2, a logarithmic trend line and error bars were added. This figure confirms the observation of Figure 1 in that better equidistance azimuth representation leads to a smaller RMS minimum and vice versa.
Figure 4: CompareOBJ's Calculated RMS With Optimal Rot. & Trans.
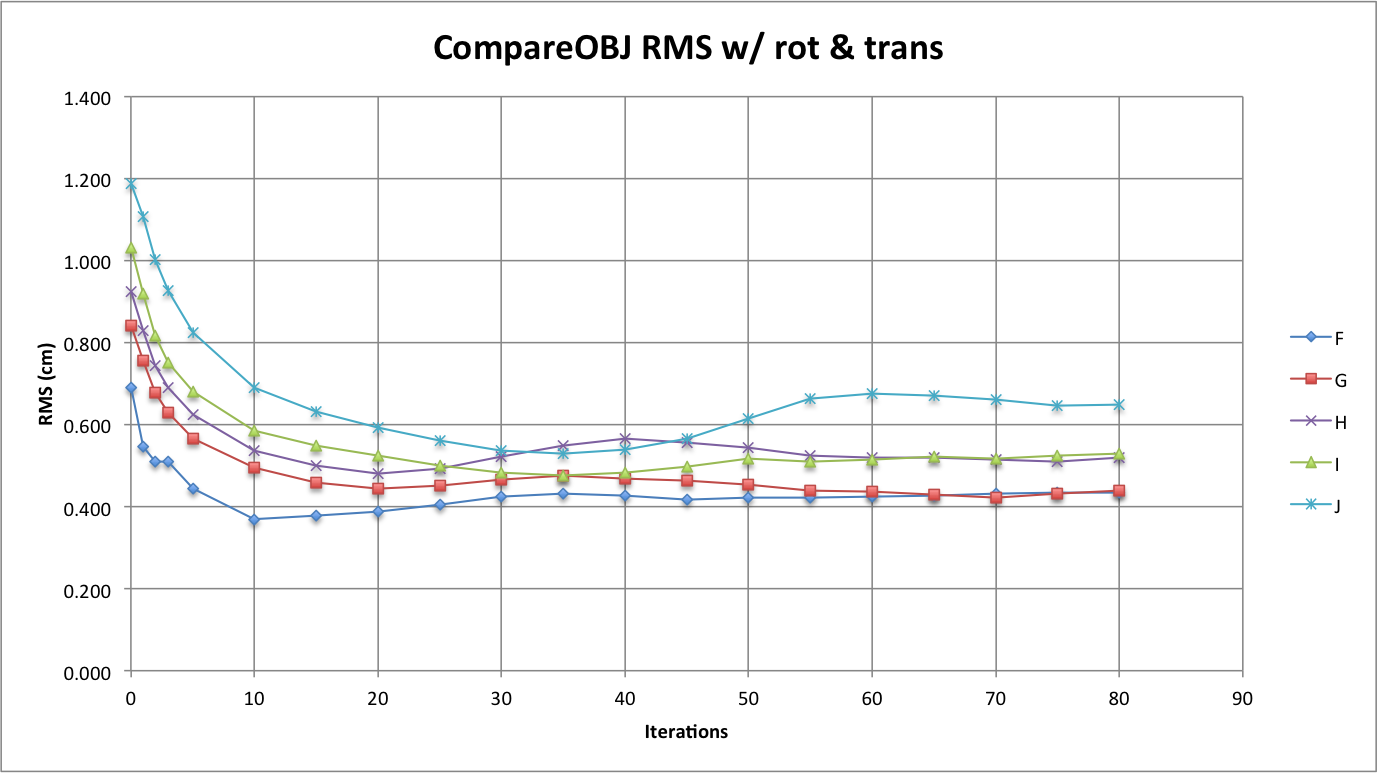
Compareing CompareOBJ's RMS with optimal rotation and translation turned on throughout the iterative process belonging to all tests shows some interesting results. For example, the RMS of Test F and G seem to be converging to the same value, which is 0.44 cm. Also, the RMS of Test I and H are converging to the same value, which is around 0.53 cm. Then there is the RMS of Test J, which is converging around 0.65 cm and is off on its own. The overall trend of the CompareOBJ with optimal translation and rotation RMS curves is that they start off at their maximum value, decrease, and then oscillate to a converging value.
When optimal translation and rotation is used with CompareOBJ, the Effort's bigmap is first transformed to the Truth's bigmap using this "optimal" translation and rotation. This means the error (RMS) calculated will be unbiased by a possible translation offset or rotation between the two models. Therefore, it makes sense that the RMS from CompareOBJ with optimal translation and rotation turned on is initially smaller and converging to a smaller value than when optimal transition and rotation is not used with CompareOBJ. That is because the Effort's topography for all tests at smaller iterations is lower than that of the Truth. When CompareOBJ with optimal translation and rotation is used, the Effort's topography is then brought up to best match the Truth. Then at larger iterations, the topography is brought down to best match the Truth. Therefore, when CompareOBJ with optimal translation and rotation is used, the RMS error being calculated is more representative of SPC's ability to handle local features since global error, like an entire Effort bigmap being offset from the Truth's, is not present.
Figure 5: CompMapVec's Calculated RMS
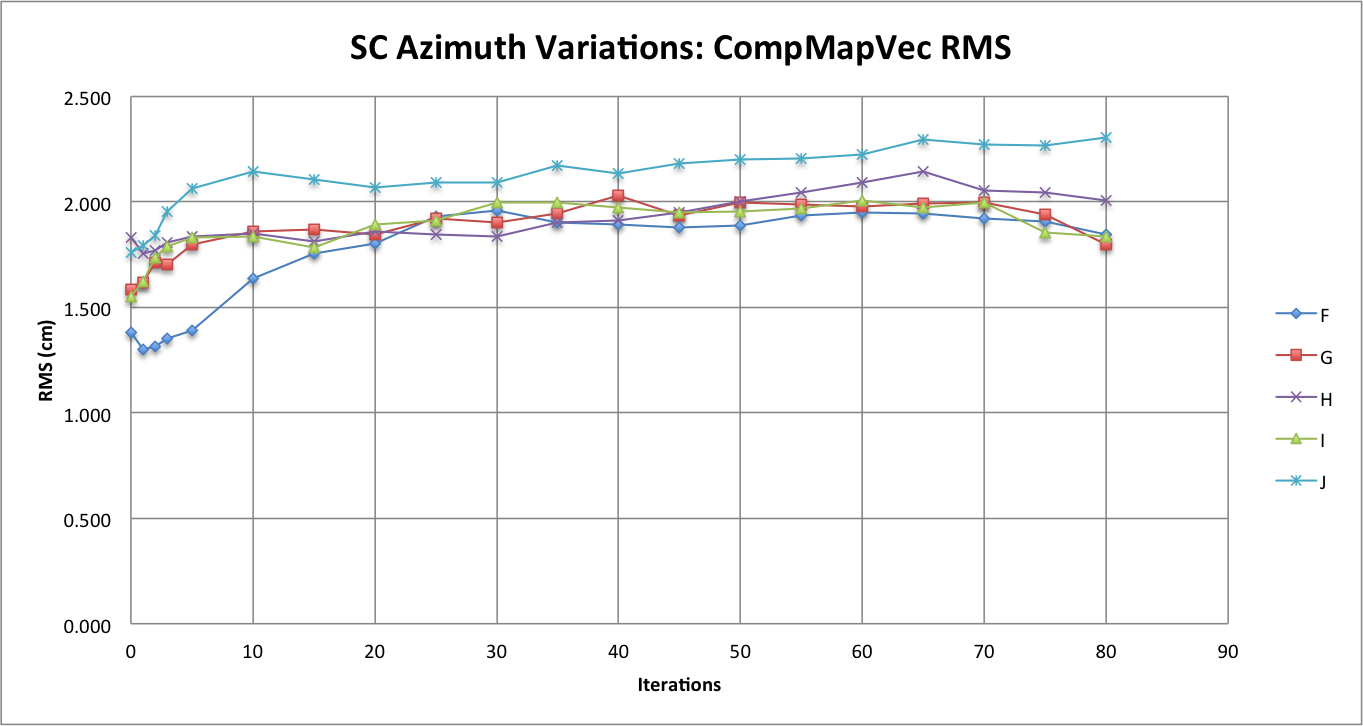
Comparing Figure 5 with Figure 1, it is clear that the RMS is calculated differently by CompareOBJ and CompMapVec. However, CompMapVec Shows better azimuthal representation leading to smaller RMS values throughout the iterative process while CompareOBJ yielded better azimuthal representation to have small RMS values before a distance minimum occurred and then better azimuthal representation caused greater RMS values to be calculated at higher resolution. I find this odd, but keep this observation in mind as I will use to analyze deviation heat maps between Effort and Truth bigmaps.
Figure 6: Measured Formal Uncertainty
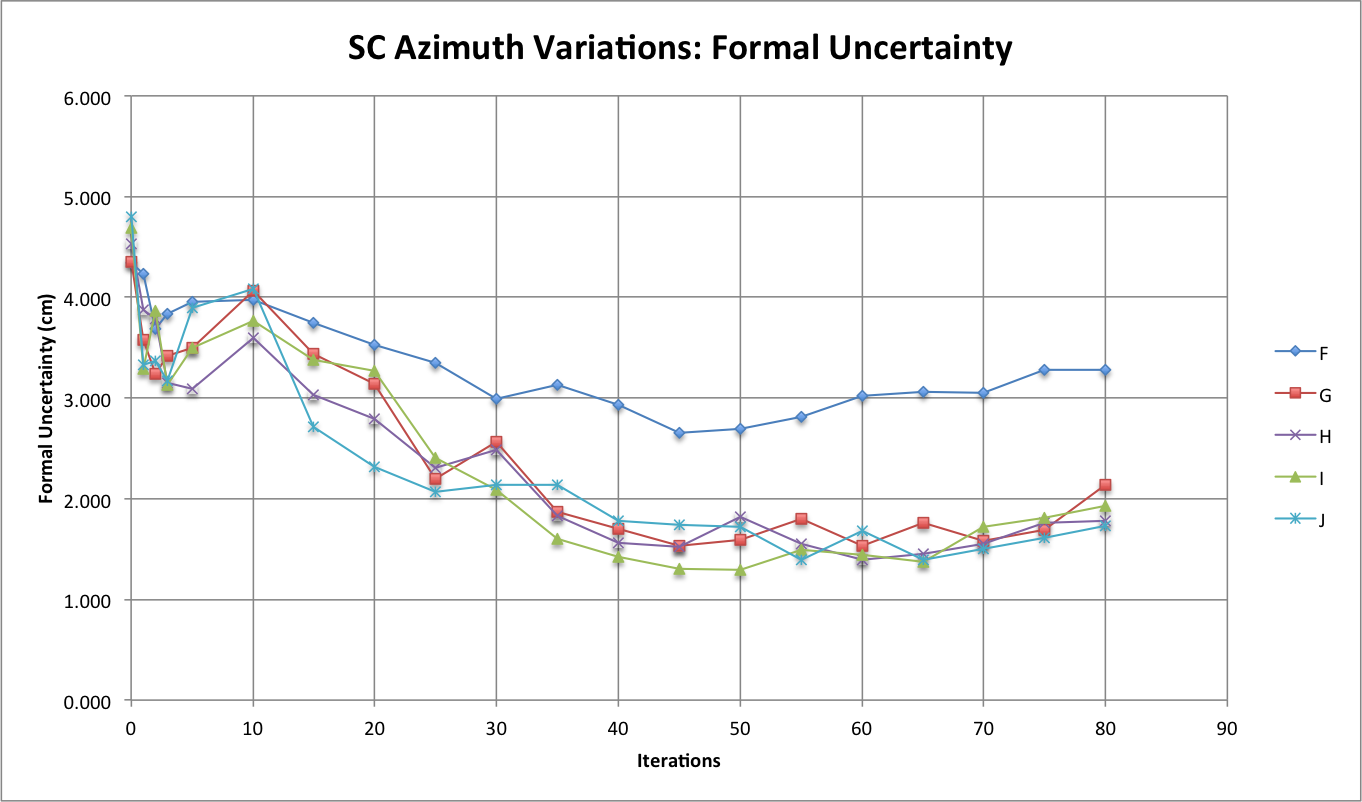
The observation that sticks out the most when comparing the formal uncertainty between the Azimuth Variations Tests is that at higher iterations the formal uncertainties for Tests G, H, I, and J seem to be hovering around one another while the formal uncertainty for Test F is about 1 cm greater than the formal uncertainty for all the other Azimuth Variation Tests. By looking at figure 1, one will also notice that CompareOBJ's calculated RMS for Test F is also the highest CompareOBJ calculated at relatively higher ( more than 30) iterations. This is interesting because Figure 5 shows CompMapVec's calculated RMS for Test F to be one of the lowest CompMapVec calculated RMS values at higher iterations. Thus, I do not think Figure 1 and Figure 5 can explain why Test F's formal uncertainty is so much higher than the formal uncertainty from all the other Azimuth Variation Tests at higher iterations when the RMS trend of those Tests are analyzed at higher iterations.
However, going back to the observations from Figure 1, it would seem that the minimum CompareOBJ RMS of Test F being the lowest and occurring the earliest my be able to explain why Test F's formal uncertainty is the greatest at greater iterations. Also, Figure 5 shows Test F's CompMapVec RMS to be the lowest at lower at iterations. Therefore, it appears that when the CompMapVec RMS and CompareOBJ RMS are relatively low, the formal uncertainty will be relatively high at greater iterations. The conclusion just made though will only occur when image azimuthal representation is better than some factor. From Figure 6, it appears that at that specific azimuthal representation factor, the formal uncertainty starts to be distinctly greater than when less azimuthal representation is present. Thus, it appears the azimuthal representation where the formal uncertainty is a lot greater is somewhere between every 30 degrees (Test G) and every 20 degrees (Test F).
Traces: North to South
The following figures are topographical transits of the test bigmaps through the center (North to South) at various iterations throughout the SPC process.
Figures 7 through 12: North to South Traces of F/G/H/I/J Tests at various iterations
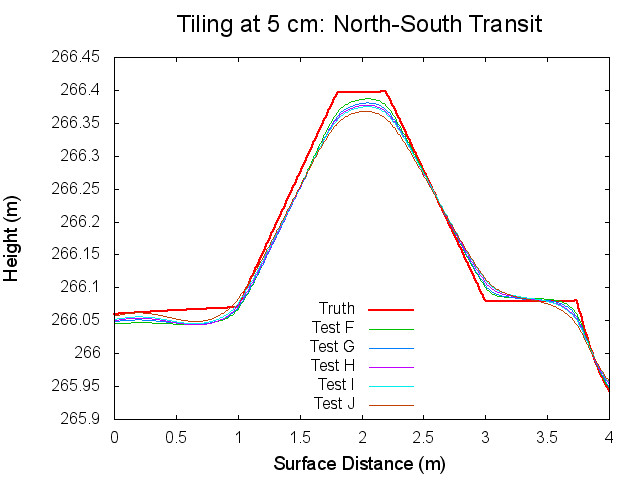
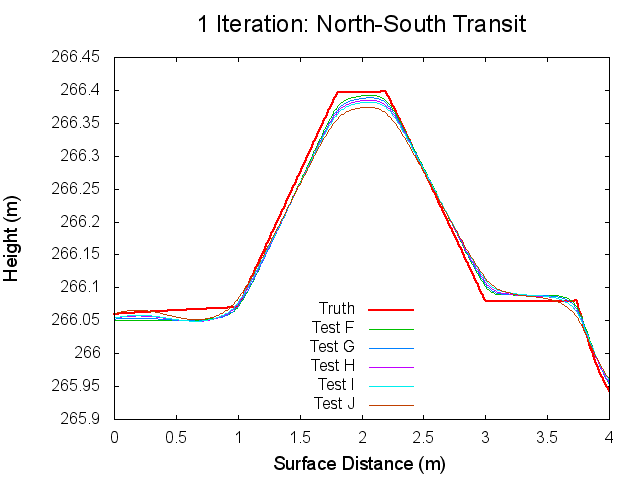
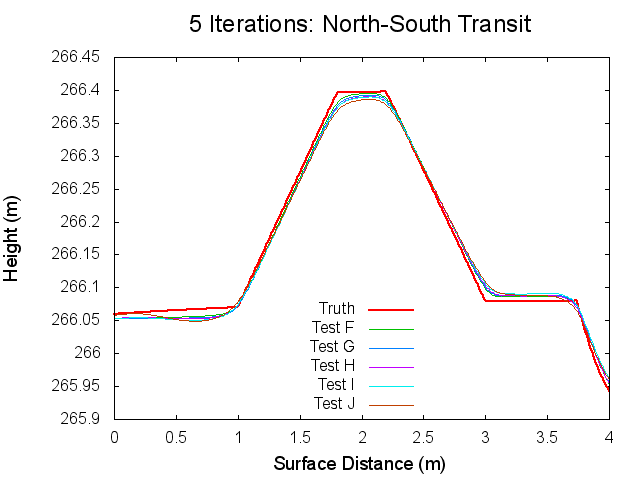
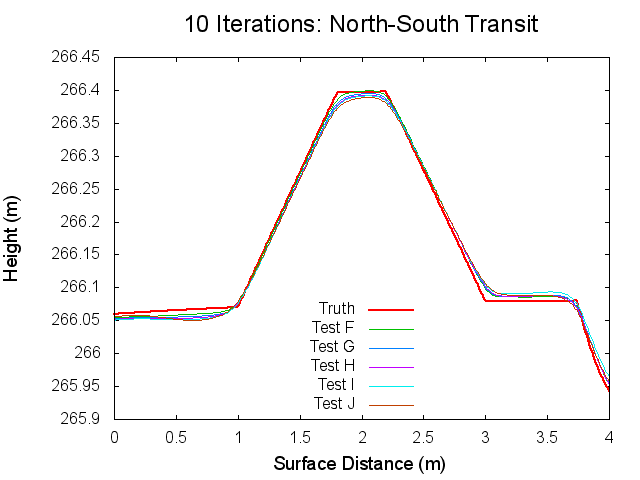
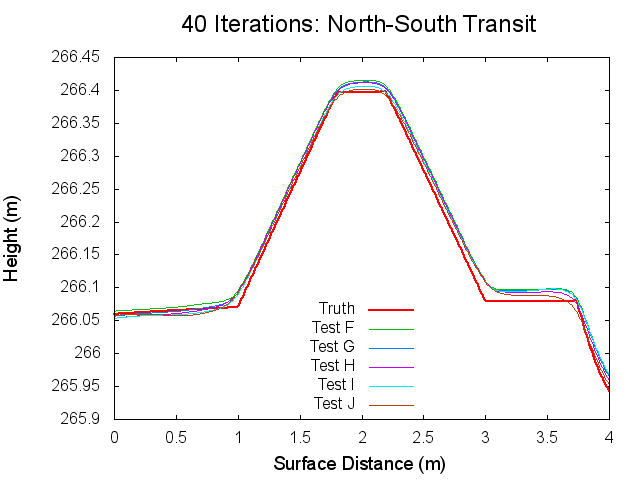
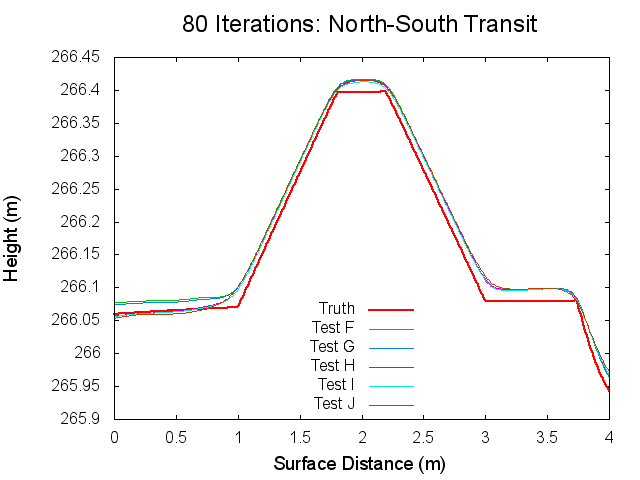
Figures 7 through 12 are great because they tie together with figures 1 through 3 in regards to observations made. By observing Figures 7 through 8 it can clearly be seen that from iterations 0 to 40, Test F produces a bigmap with a higher peak than all the other tests. At iteration 10, this peak is closest the truth, which completely falls in line with Test F's minimum CompareOBJ value observed in Figure 1 at the tenth iteration. Thus, I suspect that if I took a trace at 20 iterations Test's G and H would best represent the peak while if I took a trace and 30 iterations Test's I and J would best represent the peak. This phenomenon is occurring because, as the traces show, better azimuthal representation allows the tiling step to make better topography. The topography is initially better when images with better azimuthal representation are used because Test F represents the peak the best at iteration 0 followed by Test G, Test H, Test I, and Test J in that order. Note that at iteration 0, all the tests still under represent the height of the peak. However, once the the iteration where CompareOBJ's RMS minimum has past for a certain test, the trace for that test over represents the height of the peak. Thus, the reason why there are distinct minimums in Figure 1 is because the Effort's peak starts out lower than Truth peak, but slowly gets closer and closer throughout the iterative process, but once the Effort's peak height matches the Truth's peak height the Effort peak's height keeps on increasing with more iterations. Then of course Test F will have the earliest minimum because it's Effort peak starts out closest to the peak.
Figure 12 showing the 80th iteration is also interesting. At this iteration the height of the Effort peak for all the iterations is very close. Although, Test F and G represent the northern bast of the peak poorly, which explains why Test F and G have the greatest CompareOBJ RMS in Figure 1 at 80 iterations. Also, if you look very closely, Test I represents the peak the best. Perhaps this why Test J's CompareOBJ RMS line never crossed Test I's in Figure 1.
One more thing worth noting is that the height of the peak is always under represented at the tiling step, which falls in line with one John's tests long ago. Also note that the Southern slope all the Effort peaks is higher at the base than the Truth's. This is directly caused by the crater directly south of the peak.
Traces: West to East
The following figures are topographical transits of the test bigmaps through the center (West to East) at various iterations throughout the SPC process.
Figures 12 through 17: West to East Traces of F/G/H/I/J Tests at various iterations
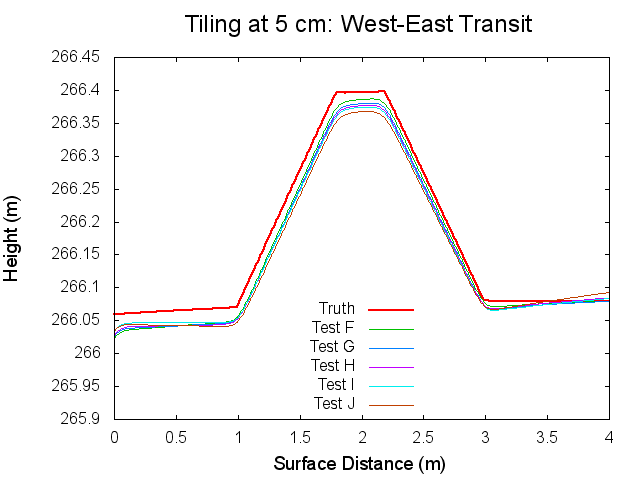
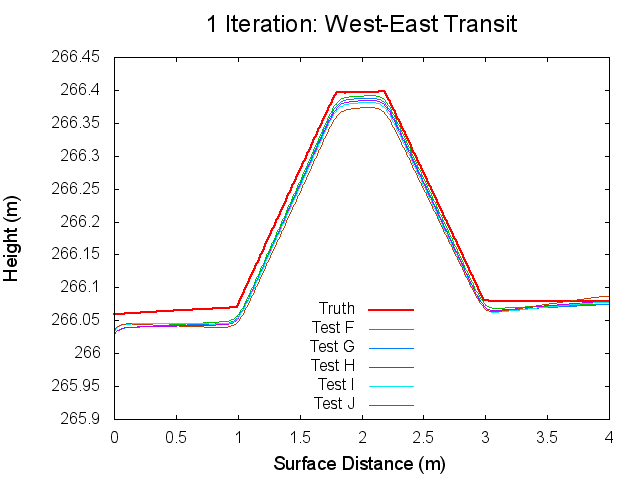
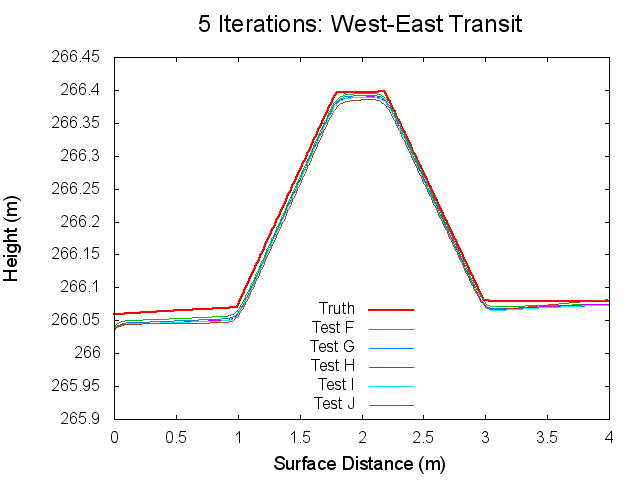
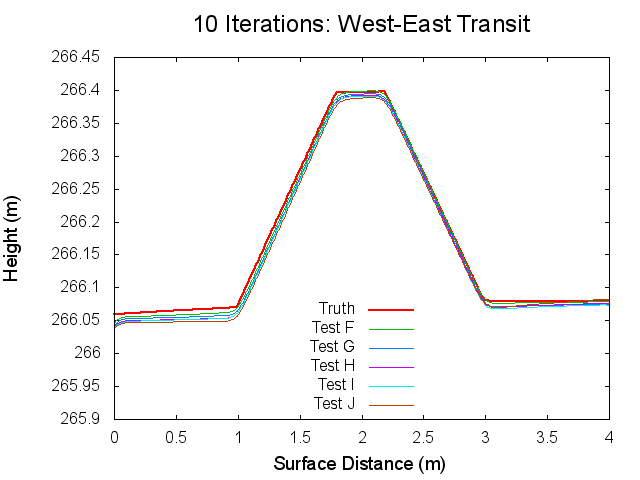
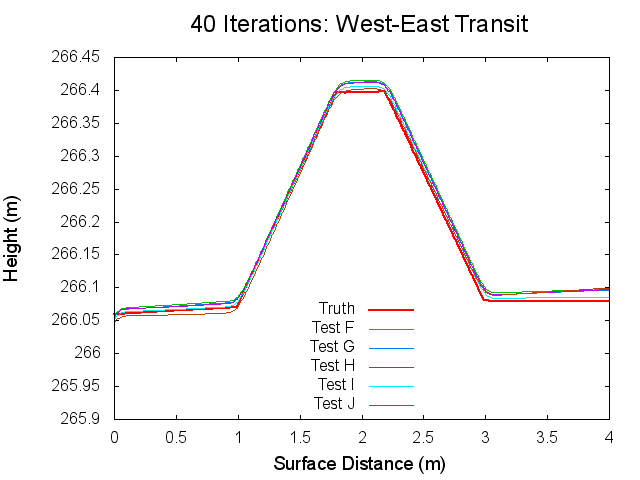
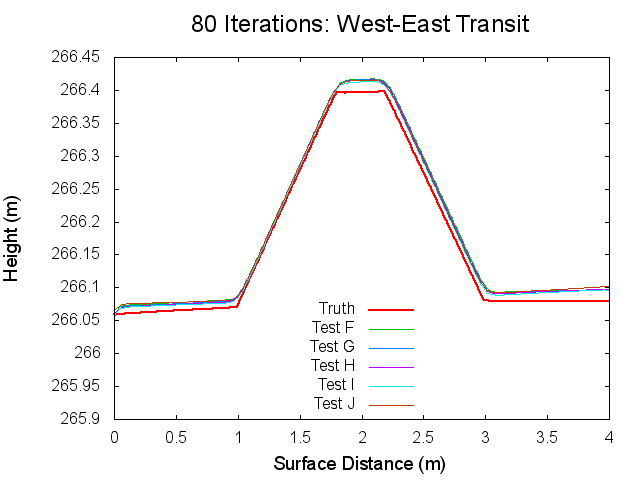
The West to East traces essentially show the same thing as the North to South traces. It is interesting though that the a slight tilt can be seen on the Truth map seen. This is possibly the curvature of the bigmap being wrapped around Bennu's surface, but I doubt that because the bigmap is small. Tilt is discussed more in the Zenith Variation Test results (Diane knows more about tit than me).
