|
Size: 3450
Comment:
|
Size: 4253
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 5: | Line 5: |
| The following two figures are line graphs that show measurements of CompareOBJ's calculated RMS with and without optimal rotation & translation at each iteration. Furthermore, figures 3 and 4 show CompMapVec's calculated RMS and the measured formal uncertainty at each iteration respectfully. Note that iteration "0" is the tiling at 5 cm step. | The following two figures are line graphs that show measurements of CompareOBJ's calculated RMS with and without optimal rotation & translation at each iteration. Furthermore, figures 3 and 4 show CompMapVec's calculated RMS and the measured formal uncertainty at each iteration respectfully. A discussion of the observations are discussed below each figure. Note that iteration "0" is the tiling at 5 cm step. |
| Line 21: | Line 21: |
| The observation that sticks out the most when comparing the formal uncertainty between the Azimuth Variations Tests is that at higher iterations the formal uncertainties for Tests G, H, I, and J seem to be hovering around one another while the formal uncertainty for Test F about 1 cm greater than the formal uncertainty for all the other Azimuth Variation Tests. By looking at figure 1, one will also notice that CompareOBJ's calculated RMS for Test F is also the highest CompareOBJ calculated RMS for all the Azimuth Variation Tests at relatively higher ( more than 30) iterations. Figure 3, also shows CompMapVec's calculated RMS for Test F to be greater than all the CompMapVec calculated RMS for all the other Azimuth Variation Tests throughout the iterative Process. Furthermore, CompMapVec's calculated RMS and CompareOBJ's calculated RMS for Tests G, H, I, and J are all closer to one another throughout the iterative process. Thus, a conclusion can made that at a specific azimuthal representation, the formal uncertainty starts to be distinctly greater than when less azimuthal representation. From Figure 4, it appears the azimuthal representation where the formal uncertainty is a lot greater is somewhere between every 30 degrees (Test G) and every 20 degrees (Test F). | The observation that sticks out the most when comparing the formal uncertainty between the Azimuth Variations Tests is that at higher iterations the formal uncertainties for Tests G, H, I, and J seem to be hovering around one another while the formal uncertainty for Test F about 1 cm greater than the formal uncertainty for all the other Azimuth Variation Tests. By looking at figure 1, one will also notice that CompareOBJ's calculated RMS for Test F is also the highest CompareOBJ calculated RMS for all the Azimuth Variation Tests at relatively higher ( more than 30) iterations. This is interesting because Figure 3 shows CompMapVec's calculated RMS for Test F to be one of the lowest CompMapVec calculated RMS values out of all the other Azimuth Variation Tests throughout the iterative Process. Thus, I do not think Figure 1 and Figure 3 can explain why Test F's formal uncertainty is so much than the formal uncertainty from all the other Azimuth Variation Tests at higher iterations when the RMS trend of those graphs are analyzed at the higher iterations. However, going back to the observations from Figure 1, it would seem that the minimum CompareOBJ RMS of Test F being the lowest and occurring the earliest my be able to explain why Test F's formal uncertainty is the at higher iterations. Also, Figure 2 shows Test F's CompMapVec RMS to be the lowest at lower at iterations. Therefore, it appears that when the CompMapVec RMS and CompareOBJ are low relatively low, the formal uncertainty will be relatively high at greater iterations. The conclusion just made though will only occur when image azimuthal representation better than some factor. From Figure 4, it appears that at that specific azimuthal representation factor, the formal uncertainty starts to be distinctly greater than when less azimuthal representation is present. Thus, it appears the azimuthal representation where the formal uncertainty is a lot greater is somewhere between every 30 degrees (Test G) and every 20 degrees (Test F). |
Test Over11 F/G/H/I/J Comparative Results
Line Graphs
The following two figures are line graphs that show measurements of CompareOBJ's calculated RMS with and without optimal rotation & translation at each iteration. Furthermore, figures 3 and 4 show CompMapVec's calculated RMS and the measured formal uncertainty at each iteration respectfully. A discussion of the observations are discussed below each figure. Note that iteration "0" is the tiling at 5 cm step.
Figure 1: CompareOBJ's Calculated RMS
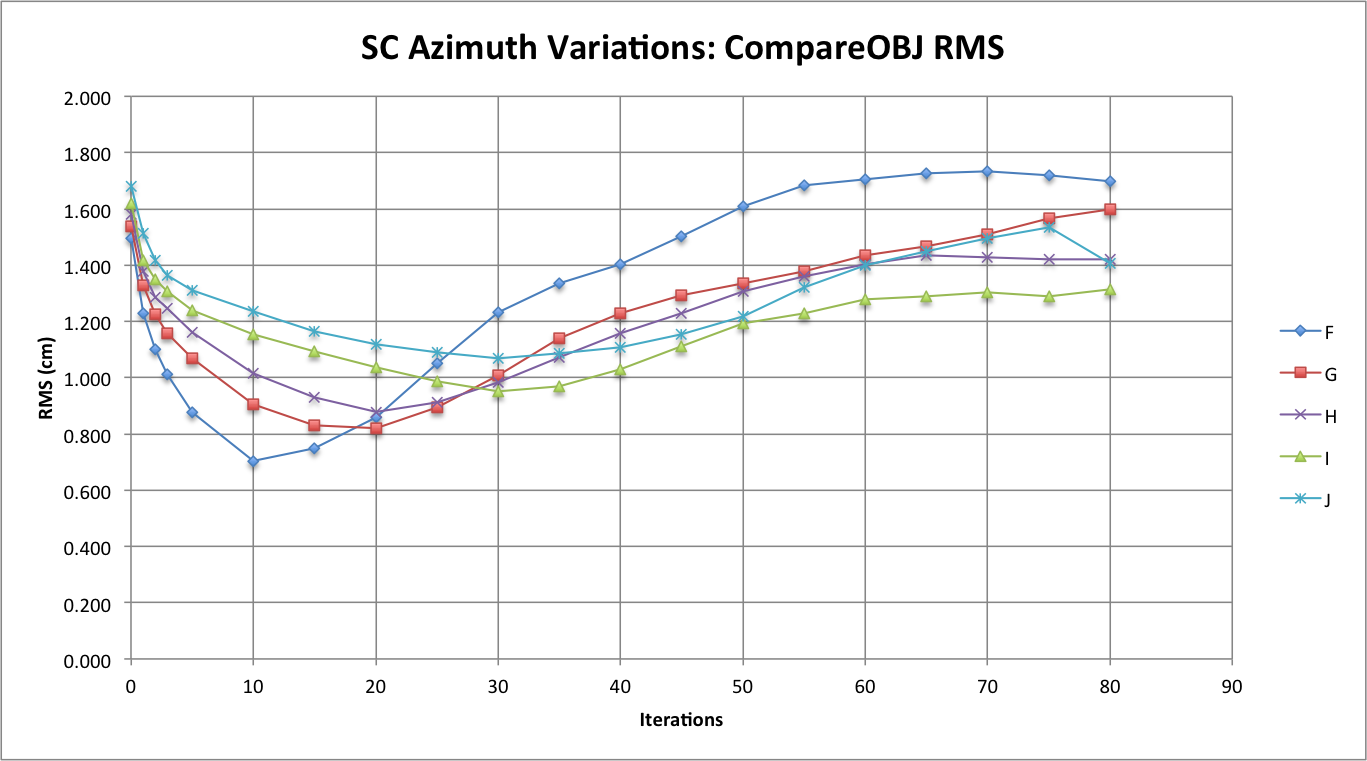
Figure 2: CompareOBJ's Calculated RMS With Optimal Rot. & Trans.
Figure 3: CompMapVec's Calculated RMS
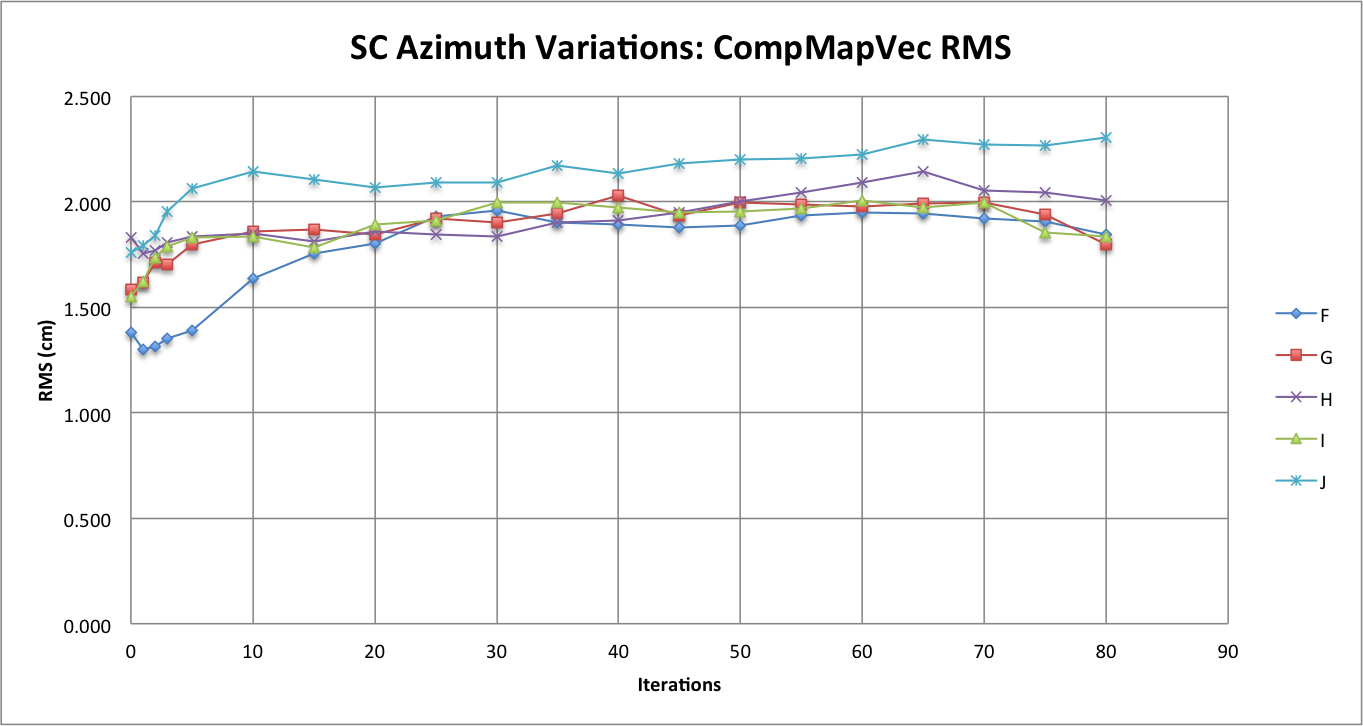
Figure 4: Measured Formal Uncertainty
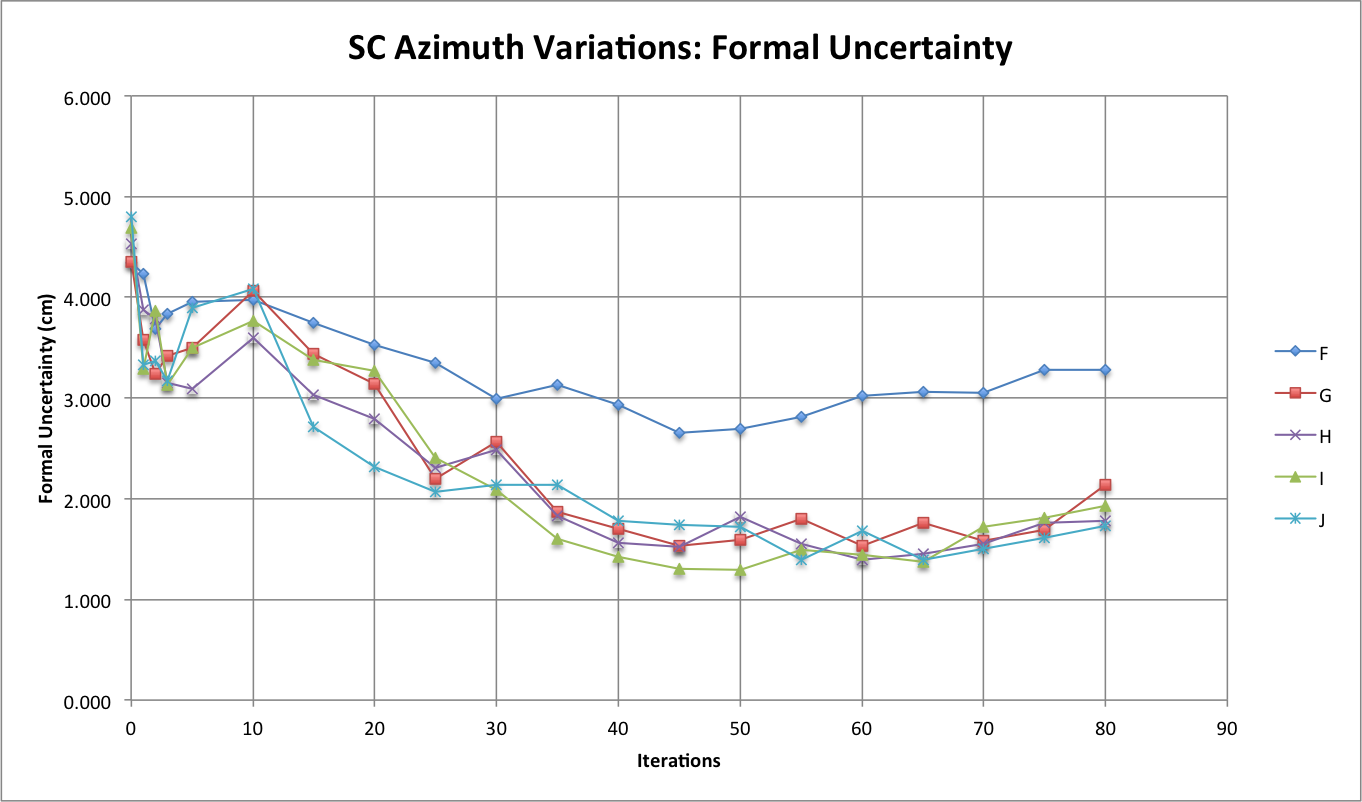
The observation that sticks out the most when comparing the formal uncertainty between the Azimuth Variations Tests is that at higher iterations the formal uncertainties for Tests G, H, I, and J seem to be hovering around one another while the formal uncertainty for Test F about 1 cm greater than the formal uncertainty for all the other Azimuth Variation Tests. By looking at figure 1, one will also notice that CompareOBJ's calculated RMS for Test F is also the highest CompareOBJ calculated RMS for all the Azimuth Variation Tests at relatively higher ( more than 30) iterations. This is interesting because Figure 3 shows CompMapVec's calculated RMS for Test F to be one of the lowest CompMapVec calculated RMS values out of all the other Azimuth Variation Tests throughout the iterative Process. Thus, I do not think Figure 1 and Figure 3 can explain why Test F's formal uncertainty is so much than the formal uncertainty from all the other Azimuth Variation Tests at higher iterations when the RMS trend of those graphs are analyzed at the higher iterations.
However, going back to the observations from Figure 1, it would seem that the minimum CompareOBJ RMS of Test F being the lowest and occurring the earliest my be able to explain why Test F's formal uncertainty is the at higher iterations. Also, Figure 2 shows Test F's CompMapVec RMS to be the lowest at lower at iterations. Therefore, it appears that when the CompMapVec RMS and CompareOBJ are low relatively low, the formal uncertainty will be relatively high at greater iterations. The conclusion just made though will only occur when image azimuthal representation better than some factor. From Figure 4, it appears that at that specific azimuthal representation factor, the formal uncertainty starts to be distinctly greater than when less azimuthal representation is present. Thus, it appears the azimuthal representation where the formal uncertainty is a lot greater is somewhere between every 30 degrees (Test G) and every 20 degrees (Test F).
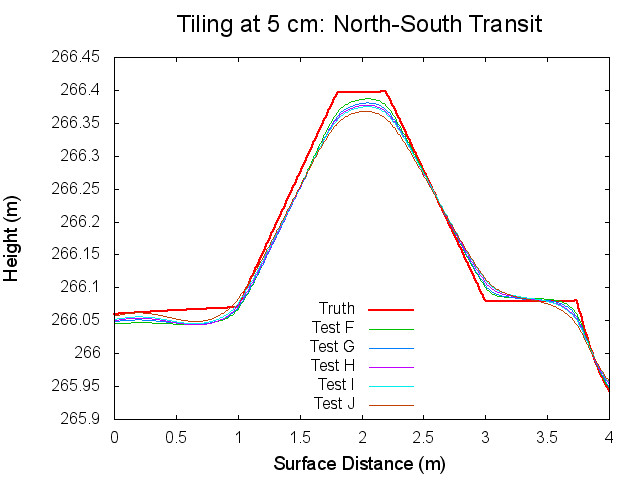
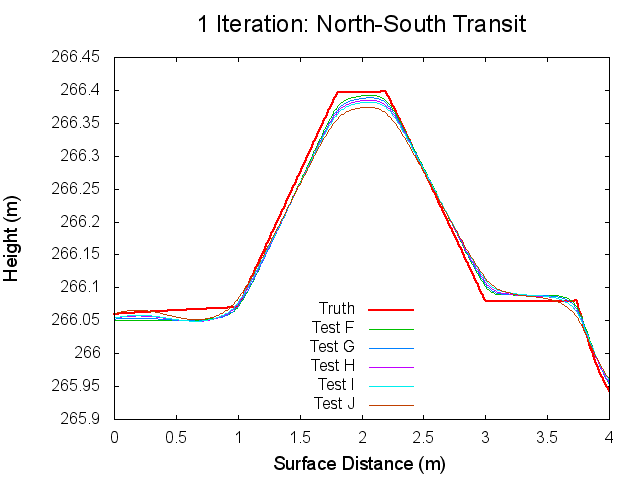
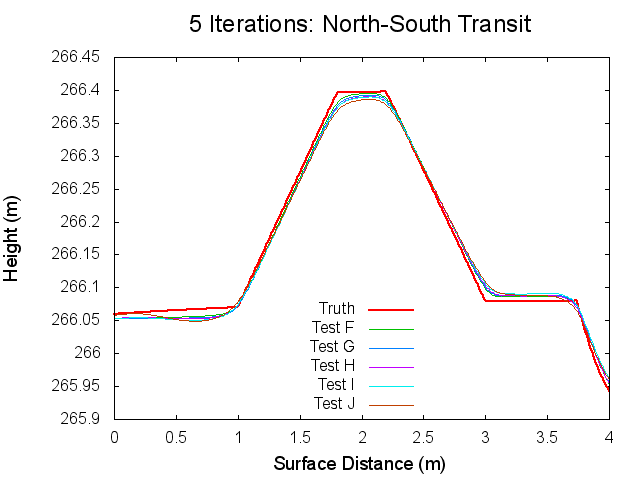
Traces: North to South
The following figures are topographical transits of the test bigmaps through the center (North to South) at various iterations throughout the SPC process.
Figures 5 through 10: North to South Traces of F/G/H/I/J Tests at various iterations
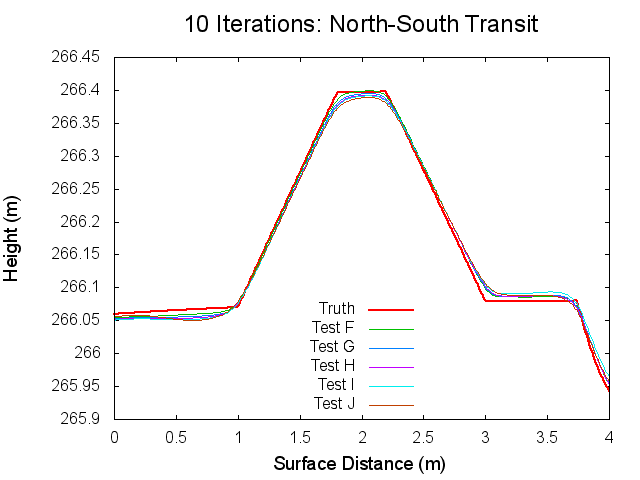
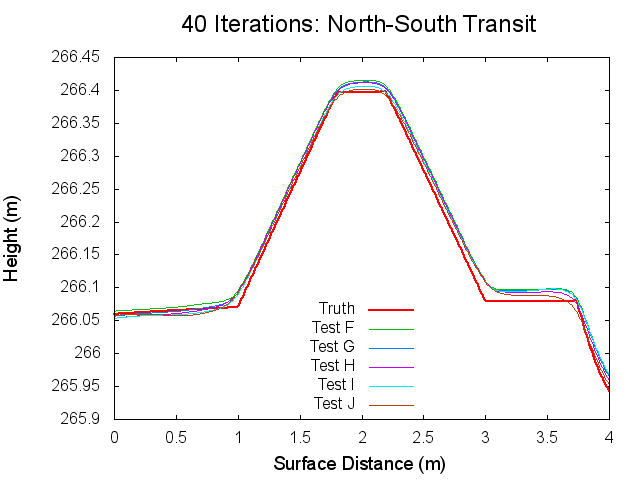
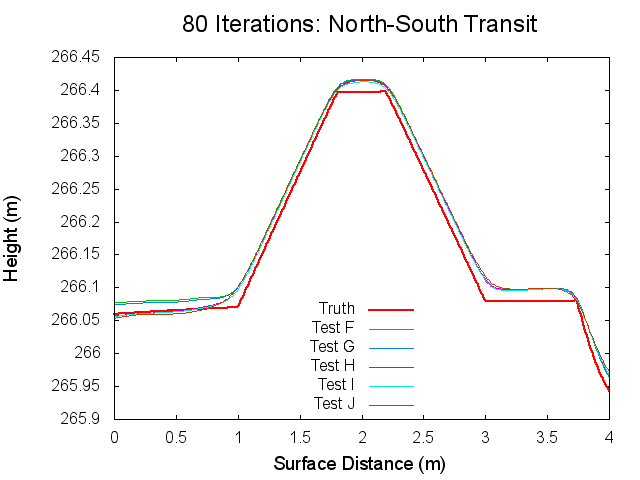
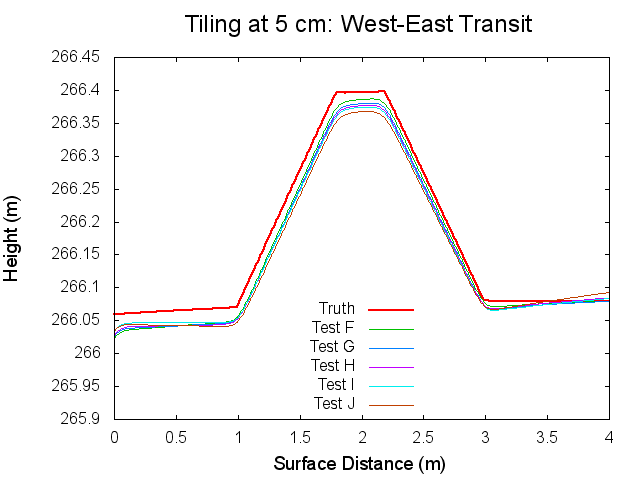
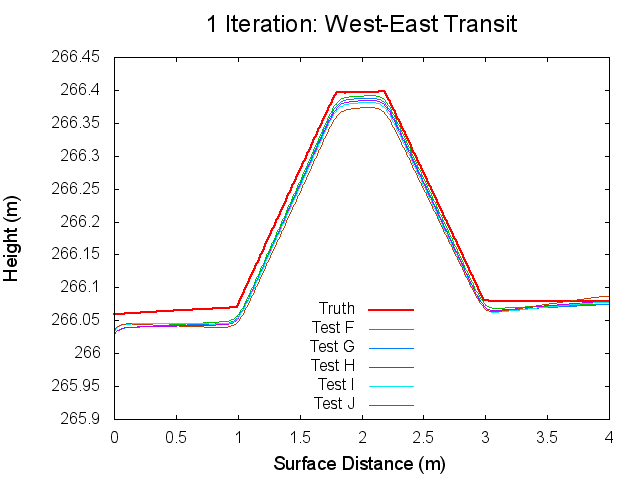
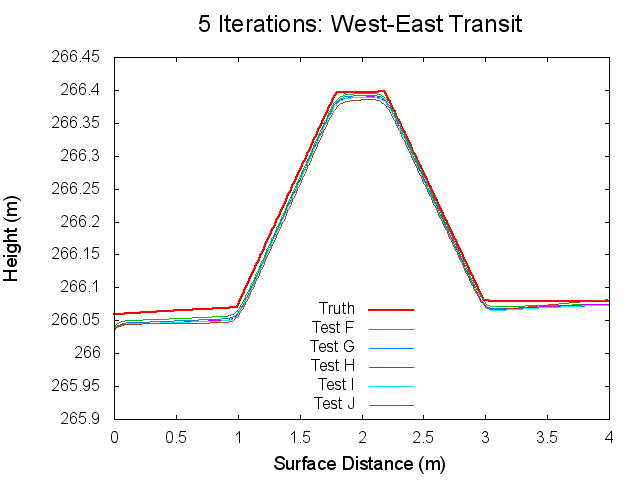
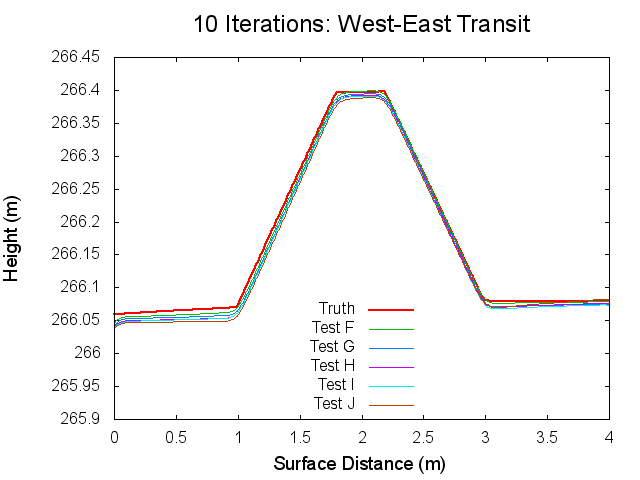
Traces: West to East
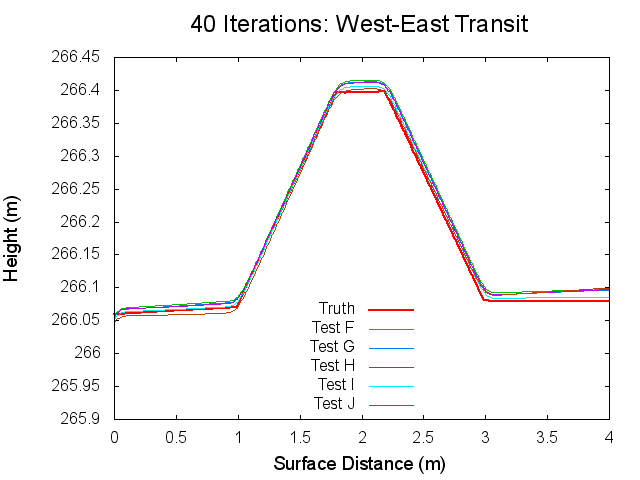
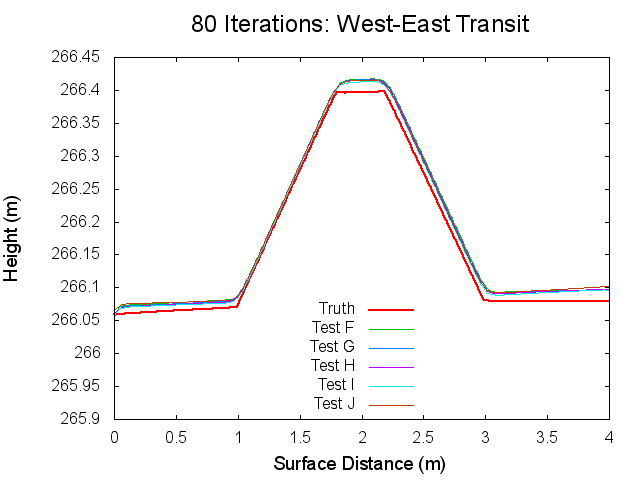
The following figures are topographical transits of the test bigmaps through the center (West to East) at various iterations throughout the SPC process.
Figures 11 through 16: West to East Traces of F/G/H/I/J Tests at various iterations